Teorema de Beal

ECUACIÓN DE BEAL

 A^x + B^y = C^z

   Para poder estudiar esta ecuación geométricamente, con las variables continuas, (x, y, z, r), es preciso partir de la aritmética :

aⁿ = b^m + c^p

que tiene las mismas soluciones que la : A^x + B^y = C^z

   Esta ecuación es imposible con tres números impares.

   Si no hay factores comunes, la ecuación impone que uno de los números, (a, b, c), sea un número par.

   Esta ecuación aritmética tiene las mismas soluciones que la geométrica :

rⁿ = x^m + y^p

·························

 

  Gráfica de la intersección de las superficies :

z = f(r) = rⁿ   (superficie de revolución)

z = x^m + y^p   (superficie, no de revolución)

en un plano paralelo al XY  y a la distancia  : z = K

 

 

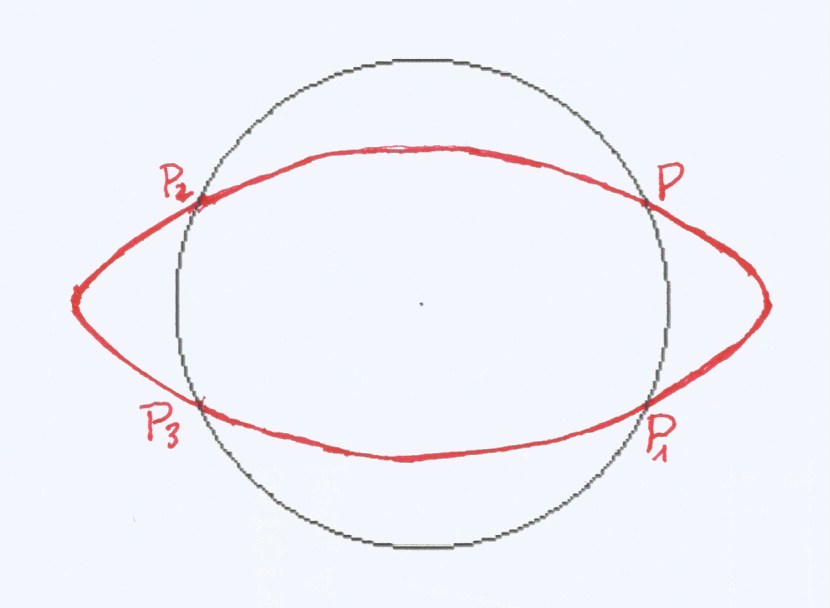
   Circunferencia, (en negro), y elipse de Beal, (en rojo), en un plano : z = K, definidas en el espacio, por los sistemas de ecuaciones :

Circunferencia   z = f(r) = rⁿ   y   z= K

Elipse                z = x^m + y^p   y   z = K

 

   Los puntos P, P₁ P₂ y P₃ están definidos por el sistema formado por estas tres ecuaciones :

P(l_x = x, l_y = y, l_z = z = rⁿ)

P(l_x = x, l_y = y, l_z = z = x^m + y^p)

P(l_x = x, l_y = y, l_z = z = K)

 

   Este sistema de tres ecuaciones define exactamente los cuatro puntos, simétricos, (P, P₁ P₂ y P₃), en un plano paralelo al cartesiano XY, que son comunes a las tres superficies, por tanto es evidente que hay soluciones aritméticas de la ecuación :

aⁿ = b^m + c^p

    AHORA BIEN, CON QUE CLASE DE NÚMEROS Y CON QUE ÍNDICES.

   Estudiemos las coordenadas de los puntos “P”, que están en la circunferencia y en la elipse.

  Recordemos que las ternas de números, (a, b, c), que verifican la ecuación :

a² = b² + c²   y   r² = x² + y²  

se conocen como ternas pitagóricas, que están formadas por las raíces cuadradas de tres enteros, y cuando las tres raíces son tres enteros, forman una terna de enteros pitagóricos,

   Las distancias del punto “P”, a los planos ZX y ZY, forman con el radio de la circunferencia un triángulo rectángulo, las tres distancias están cuantificadas por una terna pitagórica, o por un múltiplo de una terna pitagórica, por tanto con una terna de raíces cuadradas de enteros en la que, al menos, uno de los números es :

(a·√a,  b·√b  o  c·√c)   o  (r·√r,  x·√x  o  y·√y)  

   Las ternas geométricas, SIN factores comunes, que verifican la ecuación :

aⁿ = b^m + c^p   y   rⁿ = x^m + y^p  

sólo pueden tener los índices : (2,3, 2), (3,2, 2).

·························

   Comprobémoslo con algunos ejemplos de ecuaciones, con potencias de enteros, de índices mayores de dos en la ecuación :

aⁿ = b^m + c^p

29² = 5⁴ + 6³

7³ + 13² = 2⁹

2⁴ + 4⁴ = 2⁵ = 2⁴(2 = 1 + 1)

27⁴ + 162³ = 9⁷ = 3¹²(3² = 2³ + 1)

5² = 2⁴ + 3²

3² = 2³ + 1

    Ecuaciones como estas no son difíciles de encontrar, ya que todas son :

A) Cuadrados de ternas del triángulo rectángulo, (ternas pitagóricas), de la forma  (a√a, b, c), (a, b√b, c)

 o múltiplos :  m·(a√a, b, c), m·(a, b√b, c).

  B) Ternas múltiplos de la terna de Catalán, (3, 2, 1) :

  a² = b³ + 1 → 3² = 2³ + 1⁵

     Comprobemos esto en los ejemplos anteriores.

   La 1ª es el cuadrado de la terna : (29, 25, 6√6); el cuadrado de  6√6 es un entero; es evidente que : 29² = 25² + 6³, índices (2, 2,3)

   La 2ª es el cuadrado de la terna : (16√2, 13, 7√7) los cuadrados de 16√2 y de 7√7 son dos enteros;  es evidente que : (16√2)² = 7³ + 13² ; índices (2, 3, 2) 

   La 3ª es un múltiplo del cuadrado de la terna pitagórica : (√2, 1, 1)

   La 4ª es un múltiplo de la terna, de Catalán : (3, 2, 1).

   La 5ª es el cuadrado de la terna : (5, 4, 3), conocida ya por los sumerios.

   La 6ª, la de Catalán, es el cuadrado de la terna : (3, 2√2, 1), es evidente que :

  3² = 2³ + 1² índices (2, 3, 2)

     Como se puede comprobar, todas las ecuaciones aritméticas se pueden resolver con ecuaciones geométricas, en las que al menos uno de los índices es el dos, o bien tenemos factores comunes.

·························

   Las ecuaciones geométricas que resuelven las aritméticas son de la forma :

f(r) = f(x) + f(y) = r² = x² + y² 

Las geométricas en sustitución de las aritméticas, que no las resuelven, en rojo :

 29² = 5⁴ + 6³ = r² = x⁴ + y³

7³ + 13² = 2⁹ = r⁹ =  x³ + y²

2⁴ + 4⁴ = 2⁵ = r⁵ = x⁴ + y⁴

27⁴ + 162³ = 9⁷ = r⁷ =  x⁴ + y³

5² = 2⁴ + 3² = r² = x⁴ + y²

3² = 2³ + 1ⁿ = r² = x³ + 1

carecen de sentido geométrico.

Recordemos que variable independiente y función son perpendiculares :

f(x)^x, f(y)^y, f(z)^z  y f(r)^r.

Por tanto  :

z = f(r ) = r²    (1)    y    z = f(r) = r⁹   (2)

son dos funciones distintas, en (1) tenemos la coordenada de un punto en una superficie de 2º grado y en (2), tenemos la coordenada de un punto en una superficie de 9º grado.

z = f(x) = x²   (3)    y    z =f(x) = x⁴   (4)

son dos funciones distintas, en (3) tenemos la coordenada de un punto en una curva de 2º grado, en el plano XZ y en (4), tenemos la coordenada de un punto en una curva 4º grado, en el plano XZ.

   Es evidente que :

z = f(r ) = r² = 29² distinto de : z = f(r) = r⁹ = 29⁹

z = f(x) = x² = 2² distinto de : z = f(x) = x⁴ = 2⁴

   Las dos únicas ecuaciones aritméticas posibles, con tres potencias de números primos son :

5² = 2⁴ + 3²

3² = 2³ + 1   

·························

CONCLUSIÓN

   El T. de Beal es cierto. “ Es imposible la ecuación : aⁿ = b^m + c^p, sin factores comunes, con tres enteros mayores que uno y con tres índices mayores de dos”.

·························