FUNDAMENTOS DEL CÁLCULO INTEGRAL

   1º) Integrar es sumar diferenciales de los conceptos continuos : volumen V, superficie S, longitud L, ángulo a y tiempo T.

   Concepto de diferencial :

   2º) Se nomina “diferencial”, a un infinitésimo de un concepto continuo :

   3º) En un sistema cartesiano, un diferencial es un infinitésimo de una longitud, una superficie o un volumen : dv ; ds y dr

   4º) El volumen y la superficie, son conceptos que dependen de la longitud y del ángulo : V = f(l, ψ, ω)  y  S = f(l, φ) :

V = f(l, ψ, ω) = l·sen.ψ·l₁·sen.ω·l_{2 ;}   S = f(l, ψ) = l·sen.φ·l₁

   5º) En un sistema de ejes cartesianos, cuando la variable independiente “r”, toma valores en los ejes, se nomina : “x”, “y”, “z”.

    6º) La variable y su función, son ortogonales :

f(x)^x; f(y)^y; f(z)^z; f(r)^r; z = f(x); y = f(x); z = f(r_xy); r = f(x)

   7º) En un sistema cartesiano : sen.φ = sen.ω  = sen.90º = 1.

   8º) En un sistema cartesiano, las coordenadas de un punto, son las tres longitudes paralelas a los ejes, que parten de ese punto : lx = x; ly = y; z = lz .

   9º) No hay dos puntos con las mismas coordenadas

··························

      La variable longitudinal, continua, totalmente independiente es “r”.    

   Se admite que la ecuación de un paraboloide es :

z = rⁿ = (x² + y²)^n/2

pero no es cierto; z = rⁿ, define las coordenadas (l_z = z), de puntos en la superficie de un paraboloide; hay que tener presente que las coordenadas de un punto son las tres longitudes, paralelas a los ejes, que parten del punto : 

P(l_x = x, l_y = y, l_z = z = rⁿ = (x² + y²)^n/2),

   Pero ni los puntos, ni las coordenadas, (longitudes), son superficie.

·······················

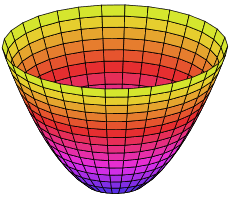
Observemos el paraboloide  de la figura :

   Estudiemos el volumen definido por la intersección del paraboloide  con un plano paralelo al cartesiano XY  y con un cilindro de radio r : (p es el número "pi")

 V(cilindro) = S·z = p·r²·rⁿ

   La intersección de este cilindro, con  base un círculo en el plano XY y centro el origen de coordenadas, con la superficie del paraboloide anterior, de altura z = rⁿ nos divide el volumen del cilindro en dos volúmenes V_z y V_xy , el 1º con base un círculo a la altura z = rⁿ = K y el 2º el de base el círculo en el plano XY; busquemos las ecuaciones que nos proporcionan los dos volúmenes :

V = S·sen.90º·z = V_z + V_xy

V = p·r²·sen.90º·z = p· r²· rⁿ = V_z + V_xy

   Veamos como varía “V”, cuando varía “r” :

V + dv = p· (r + dr)²· (r + dr)ⁿ

(r + dr)²·(r + dr)ⁿ = (r² + 2·r·dr + dr·dr)·(rⁿ + n·r^n-1·dr + n·(n-1)·dr·dr + n·(n-1)·(n-2)·dr·dr·dr +······+ drⁿ)

 dr·dr = 0

 n·(n-1)·dr·dr + n·(n-1)·(n-2)·dr·dr·dr+ ··+drⁿ = 0

 V + dv = p·(rⁿ⁺² + (n + 2)·rⁿ⁺¹·dr)

dv = p·(n + 2)·rⁿ⁺¹·dr = n·p·rⁿ⁺¹·dr + 2·p·rⁿ⁺¹·dr

“dv” varía en la proporción de “n” a “2”.

∫dv = ∫ p·(n + 2)·rⁿ⁺¹·dr = p·(n + 2)·rⁿ⁺²·r/¿w? =  V

V = p· r²· rⁿ

Es evidente que : ¿w? = (n + 2) 

∫dv = ∫p·(n + 2)·rⁿ⁺¹·dr = p·(n + 2)·rⁿ⁺¹·r/(n+2) =  V

V = (n+2r⁽ⁿ)·p·rⁿ⁺²⁾/(n+2) = p·r⁽ⁿ⁺²⁾

 V_z = n·p·r⁽ⁿ⁺²⁾/(n+2) ; V_xy = 2·p·r⁽ⁿ⁺²⁾/(n+2)

   EJEMPLO :

z = r³ = 2³

V = p· r²· rⁿ = V = p· 2²· 2³ = p·32 (udv)

V_z = n·p·r⁽ⁿ⁺²⁾/(n+2) = 3·p·2⁽³⁺²⁾/(3+2) = p·32·(3/5) (udv)

V_xy = 2·p·r⁽ⁿ⁺²⁾/(n+2) = 2·p·r⁽²⁺²⁾/(2+2) = p·32·(2/5) (udv)

p·32·(3/5) (udv) + p·32·(2/5) (udv) = p·r²· r³ = V

·························